[CO2412 Computational Thinking Contents]]
Lecture 11 - Inheritance Based Structures - Interfaces

Lecture 11 - Inheritance Based Structures & Interfaces.pdf

Probability¶

The meaning of probability could be described as below:

Probability¶

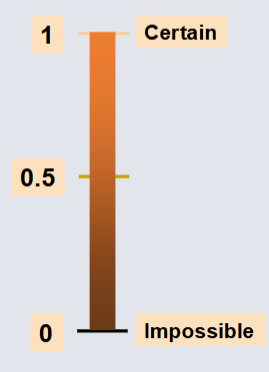
Probability is the numerical measurement of the likelihood of an event to occur.

The probability of any event must be between 0 and 1 inclusively.

P(A) = Probability(Action)
0 <= P(A) <= 1 (For any event A)

There are three generally accepted classes of probability:
- Logical or Classical Probability
- Frequentist or Observed Probability
- Subject Probability

Logical or Classical Probability¶

The probability of an Event A can be formally defined as:

P(A) = Number of outcomes that lead to Event A / Total Number of possible outcomes

This is an objective number e.g. probability of observing tails when a coin is tossed is 1/2 or 0.5 or 50% or 1 to 1 or 1 in 2.

Frequentist Probability 'Law of Large Numbers'¶

What is the probability that a randomly selected man earns more than 50K?

In many situations it is not possible to determine the 'logical' probability of an event however, it is possible to calculate the probability as long as it is possible to study the event many times under reasonably identical conditions.

As such, this is the most common way of determining probability because as long as the situation can be repeated many times, under reasonably identical conditions.

Then the probability can be calculated this way as a result.

Thus in then long run, the probability of an event A can be defined as:
P(A) = Frequency of event A / Total number of observed events.

Subject Probability¶

(First) Consider this objectively:¶

You are sitting on a selection panel.

You're considering candidate X's suitability.

What is the probability that candidate X will be successful in the position if selected?

Need for Subject Probability¶

In many situations it is not possible to determine the frequency of an event objectively:
- An event cannot successfully duplicated e.g. one-off project say Candidate X
- Duplication is too costly, too slow, inefficient (i.e. benefit minimal)
- Duplication is too complex e.g. if event depends on other events.

Common Problems: Subjective Probability¶

The interpretation of the language of uncertainty, differs among individuals. Most individuals find it hard to quantify uncertainty: especially true of very rare events for which event the possibility-hood is hard to visualise or predict.

Example¶

It is September 10th 2001. What is the probability of men flying a hijacked plane into a high rise building?

Judgement of probability is coloured by the information available: consider for example a doctor treating a patient with unknown symptoms.

Consequently, vivid events often judged more likely than they are: experiments show, for example that most people think accidents cause as much death as disease yet the latter is much more likely to cause death than the former.

Elementary Probability¶

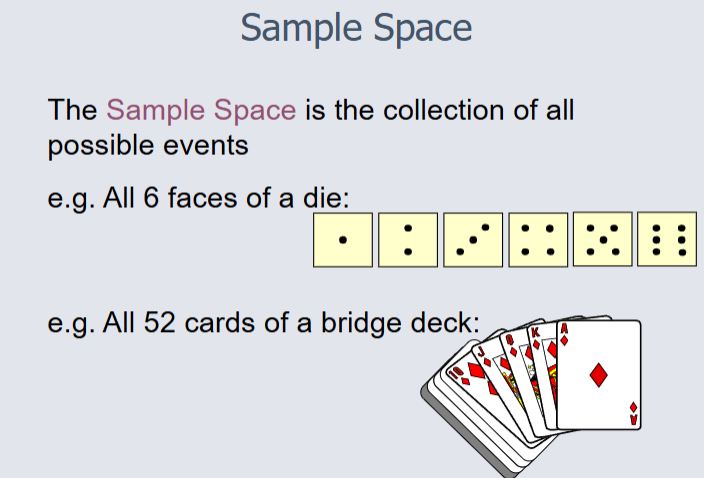
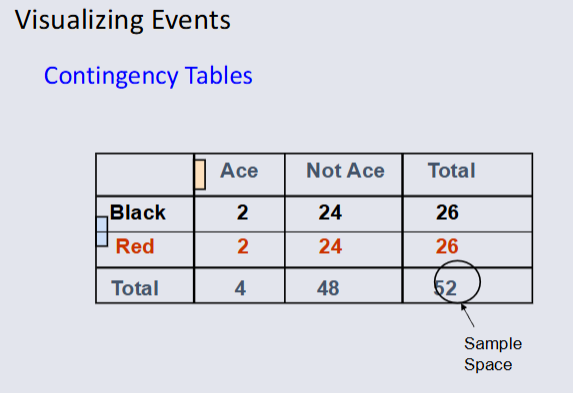
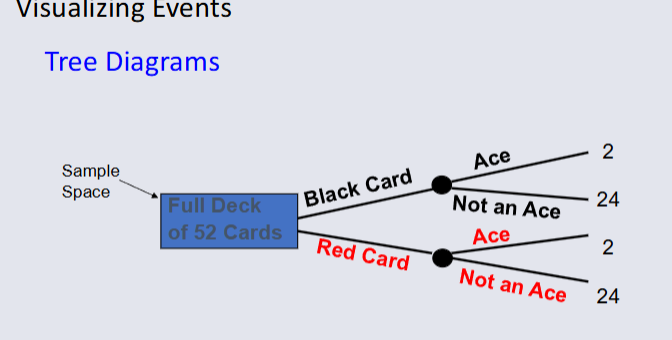
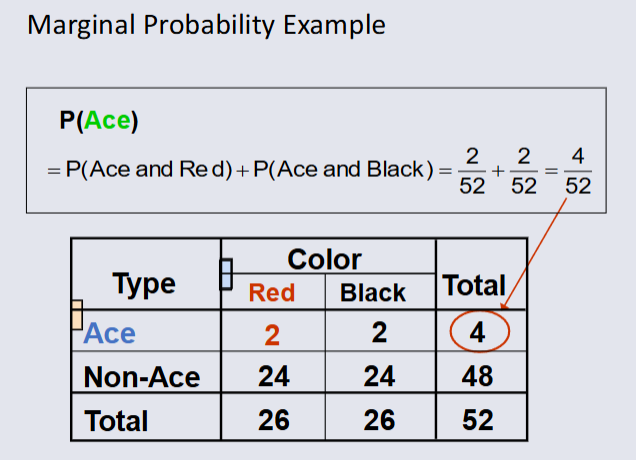
Computing Joint Possibility¶

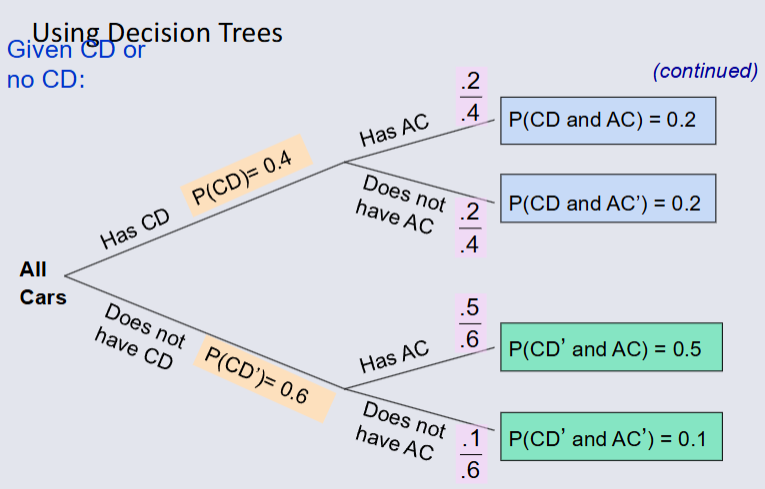
The possibility of a joint event A and B:
P(A and B) = number of outcomes satisfying A and B / total number of elementary outcomes
![[Joint Probability Example#.png]]

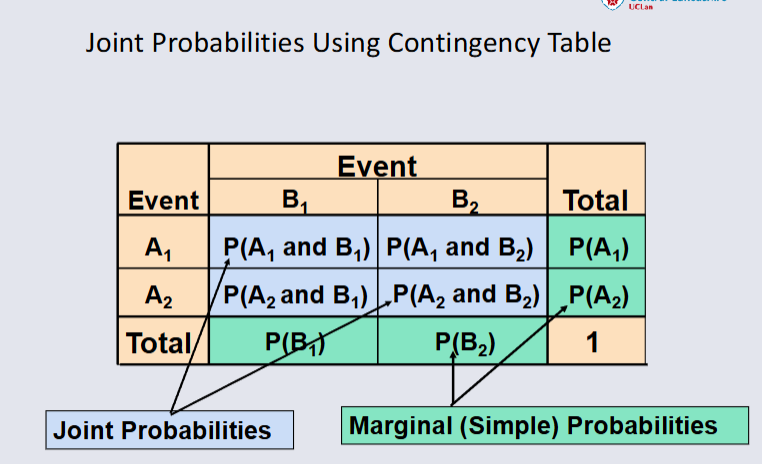
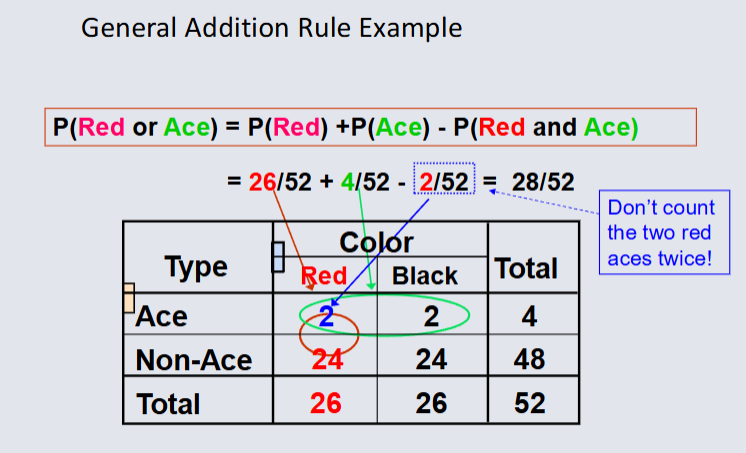
The General Addition Rule¶

P(A or B) = P(A) + P(B) - P(A and B)

Simplification of the Addition Rule¶

When events are Muturally Exclusive Events i.e. they cannot happen simultaaneously.

P(A and B) = 0

Hence the Addition Rule simplifies to:
P(A and B) = P(A) + P(B)

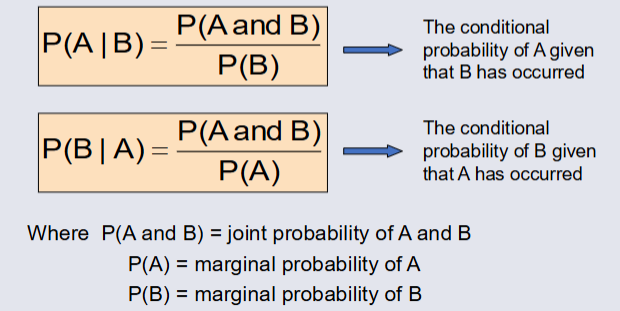
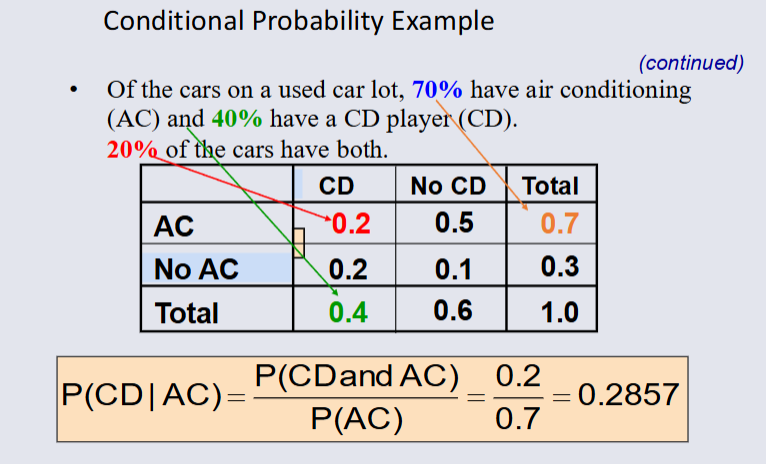
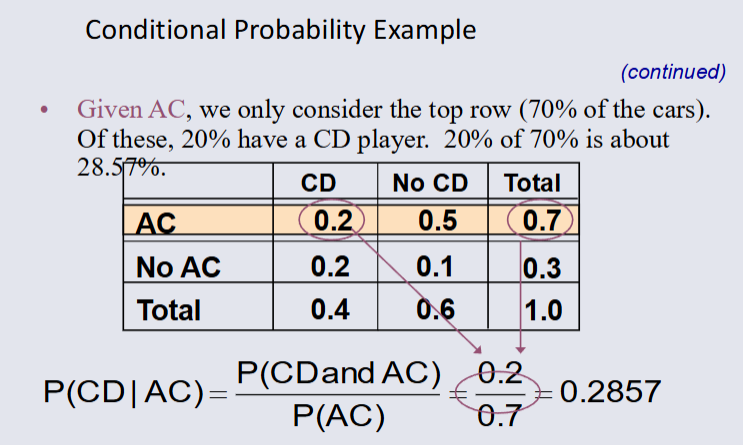
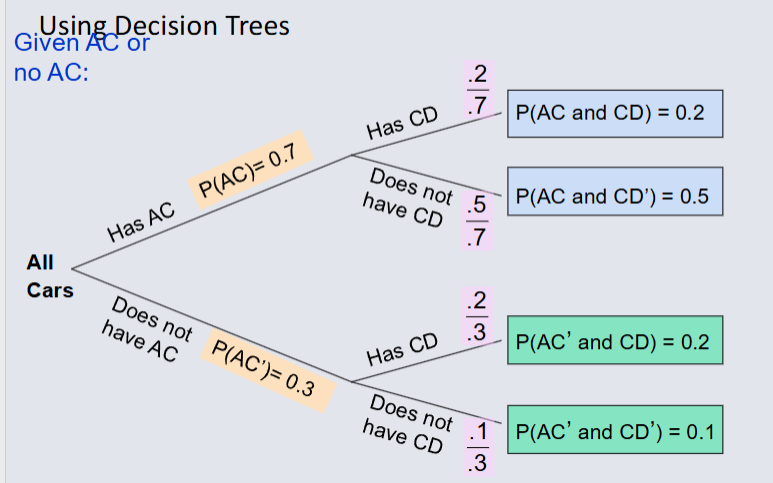
Computing Conditional Probabilities¶

A conditional probability is the probability of one event given that another event has occured:







Lecture 13 - Info Representation