CO2412¶

Computational-Thinking¶

CO2412 Computational Thinking Contents
Lecture 13 - Info Representation

Lecture 14 - Numeric Data Analysis.pdf

Numeric Data Analysis¶

Learning Objectives¶

Describe the properties of Central Tendency, Variation, and Shape in Numerical Data.

To calculate descriptive summary measurements for a population.

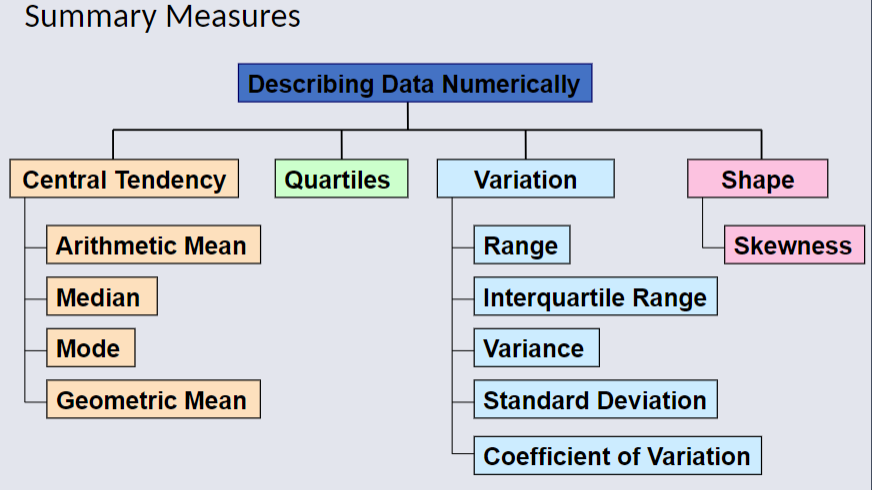
Measures of Central Tendency, Variation, and Shape¶

Mean, Median, Mode, Geometric Mean
Quartiles
Range, Interquartile Range, Variance, and Standard Deviation, Coefficient of variation, Z-Scores
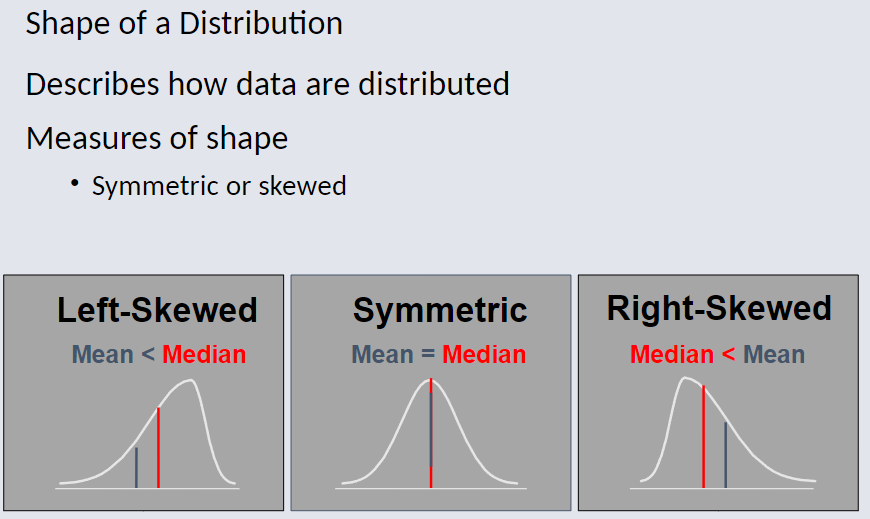
Symmetric and Skewed Distributions

Population Summary Measures¶

Mean, Variance, and Standard Deviation

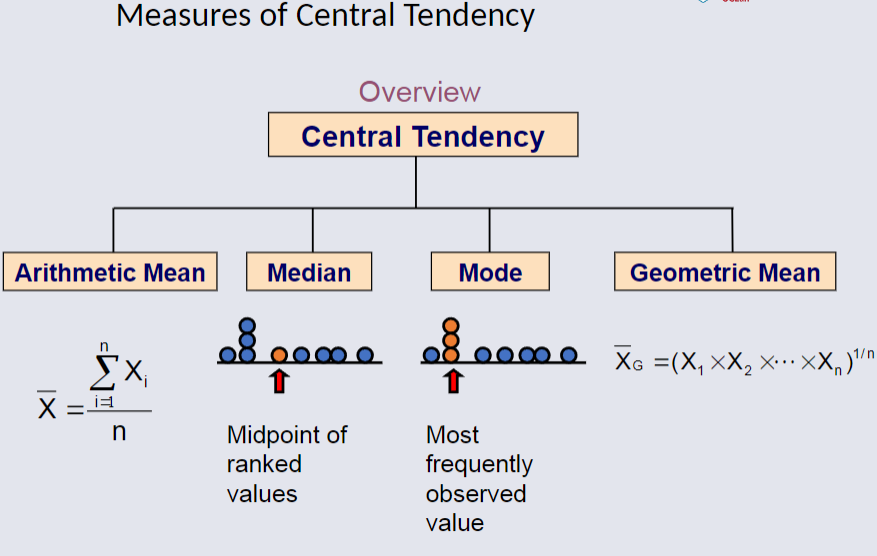
Arithmetic Mean¶

The arithmetic mean (sample mean) is the most common measure of central tendency.

For a sample of size n:
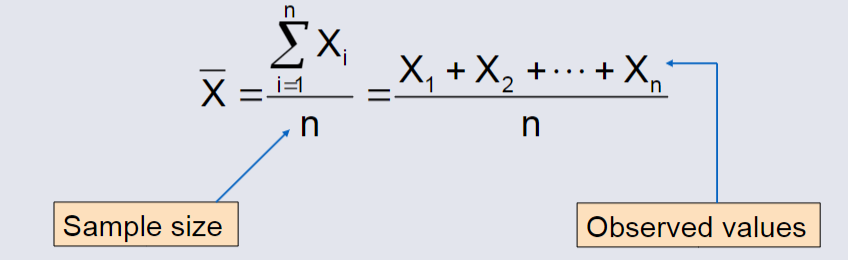
Arithmetic Mean.png
The most common measure of central tendency.
Mean = sum of values divided by the number of values.
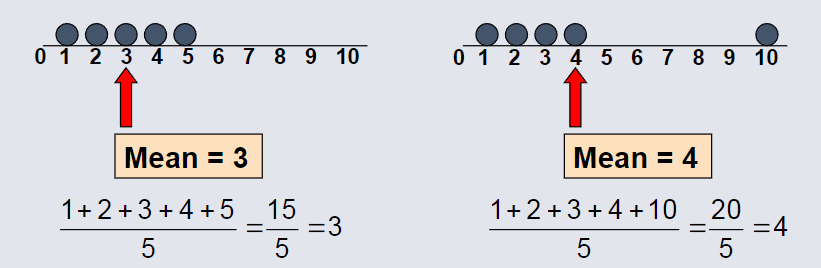
Mean positioning.png

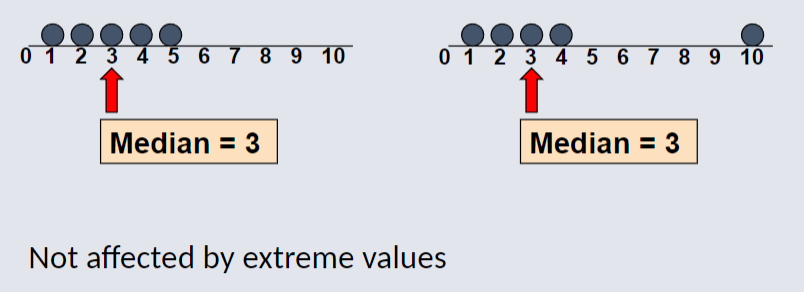
Median¶

In an ordered array, the median is the middle number (50% above, 50% below).
Median positioning.png

Finding The Median¶

The location of the median uses the following formula:
Median Position = (n + 1) / 2
N being the position in the ordered data.
median position quartiles.png

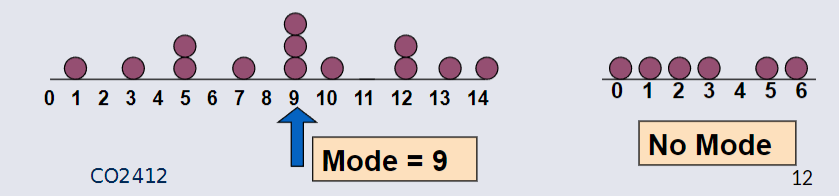
Mode¶

A measurement of central tendency.
Value that occurs most often, and is not effected by extreme values.

Used for either numerical or categorical data.
There may be no mode.
There may be several modes.

Example Mode¶

Mode and no Mode Example.png

Review Example: Summary Statistics¶

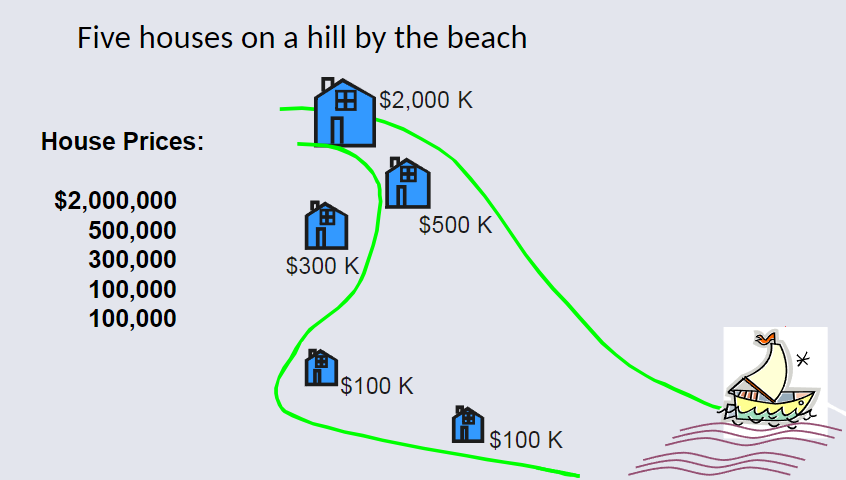
house Example.png
Mean: 3000000 (total sum of house prices) / 5 (total amount of houses)
Median: Middle value of ranked data: 300000
Mode: Most Frequent Value = 100000

Which measure of location is best¶

Mean is generally used, unless extreme values (outliers) exist.
Median is second often used since the median is not sensitive to extreme values.

In regards to median with House Example:
Median home prices may be reported for a region as it is less sensitive to outliers.

Quartiles¶

Quartiles split the ranked data into 4 segments with an equal number of values per segment.

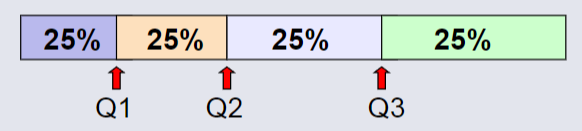
The first quartile Q1 is the value for which 25% of the observations are smaller and 75% are larger.
The second quartile Q2 is the same as the median (50% are smaller, 50% are larger)
Only 25% of the observations are greater than the third quartile Q3.

Quartile Formulas based on Example¶

Q1 = (n + 1) / 4
Q2 = (n + 1) / 2 (The Median Position)
Q3 = 3(n + 1) / 4
Example First Quartile.png
Example Ordered Array.png

Measures of Variation¶

Range¶

Simplest measure of variation.
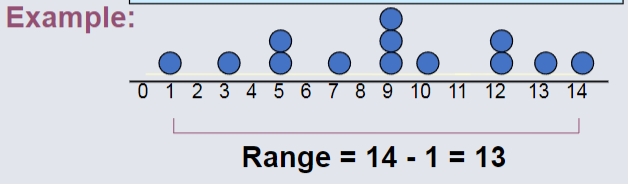
Difference between the largest and the smallest values in a set of data:
Range = Largest Value - Smallest Value

Example Range¶

Example Range.png

Disadvantages of Range¶

Ignores the way in which data is distributed.
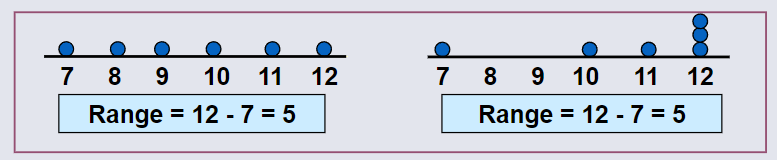
Sensitive to Outliers

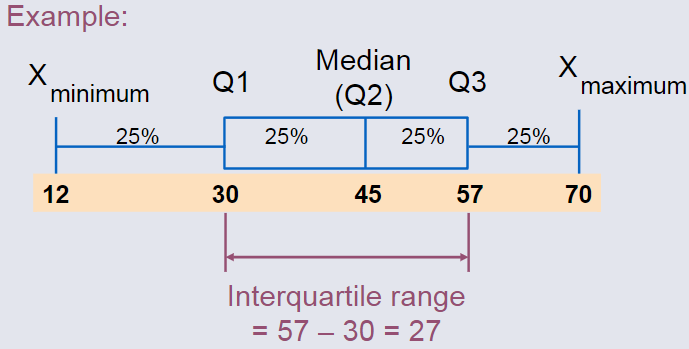
Interquartile Range¶

Can eliminate some Outlier problems by using the Interquartile Range.

Eliminate some high- and low-valued observations and calculate the range from the remaining values.

Interquartile Range = 3rd Quartile - 1st Quartile

Example Interquartile Range¶

Example Interquartile Range.png

Variance¶

Average (Approx) of squared deviations of values from the mean.
Simple Variance.png

Standard Deviation¶

Most commonly used in measure of variance.
Shows variation about the mean
Has the same units as the original data
Simple Standard Deviation.png

Example Standard Deviation¶

Sample Average Mean Data for Standard Deviation.png

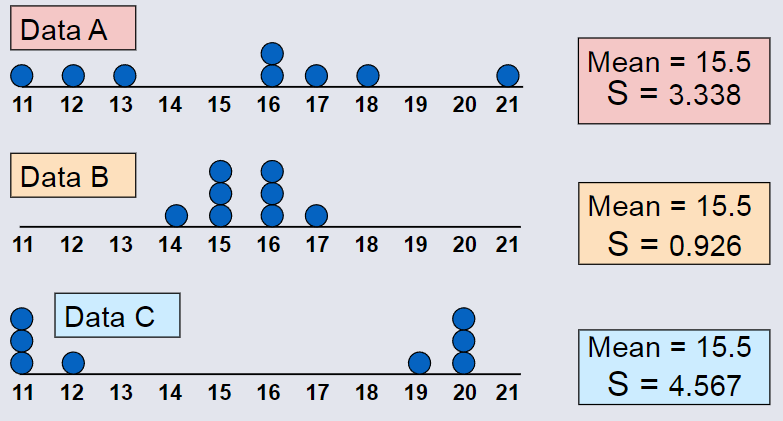
Measuring Variation¶

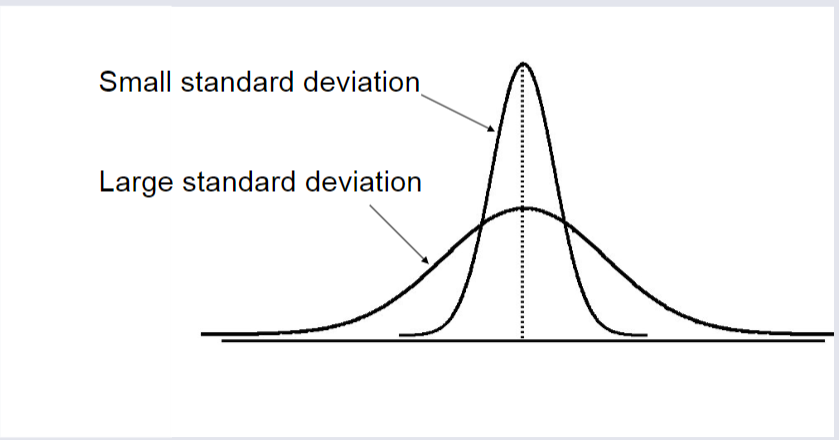
Distibution Meanings.png

Comparing Standard Deviations¶

Advantages of Variance and Standard Deviation¶

Each value in the dataset is used in the calculation
Values far from the mean are given extra weight (Because deviations from the mean are squared)

Coefficient of the Variation¶

Measures relative variation.
Always in Percentage (%)
Shows Variation Relative to Mean
Can be used to compare two or more sets of data measured in different units.
![[Pasted image 20250426223524.png]]

Comparing Coefficient of Variation¶

Standard Deviation Example.png

Shape of Distribution¶

Shape of Distribution.png