CO2412 Computational Thinking Contents
Lecture 4 - Sort Algorithms
Lecture 5 - Greedy_Branch_Bound.pdf
Greedy & Branch and Bound¶
The Greedy Algorithm¶
The Greedy Algorithm always selects the most advantageous option at each step, without considering the impact of previous decisions or future consequences.
While this approach is straightforward and can be effective, it isn't guaranteed to yield an optimal solution in the 0/1 knapsack problem because it doesn't account for the broader picture.
However, if the 0/1 knapsack problem is modified to become a fractional knapsack problem, where items can be divided into smaller portions, the Greedy Algorithm becomes an optimal solution.
This is because the algorithm prioritizes items based on their value-to-weight ratio, ensuring the maximum gain for the available capacity.
Different way to maximise profit¶
So far profit/value has been maximised by simply taking the highest value available and oversing the weight constraint.
A better measurement could be the profit per unit of weight.
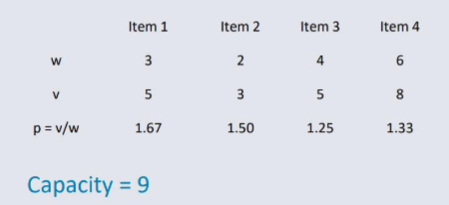
Fractional Knapsack¶
1) Take the highest ranked item in term until the knapsack is full
2) The Highest ranked item is Item 1 with a profit of 1.67 so add it to the knapsack
3) The next highest ranked item is Item 2 with a profit of 1.5
4) The knapsack now contains Item 1 + 2 which has a weight of 5 and value of 8
5) The next best item is Item 4 (Profit = 1.33) but it doesn't fit therefore a fractional knapsack allows the part being carried to be used
Fractional Knapsack 0/1¶
Capacity (9) - Current Weight (5) = 4
4(8/6) = 5.32
Best Solution is Item 1, Item 2, and Item 4.
Weight = 9
Value = 13.32
Fractional & 0/1 Knapsacak¶
The fractional Knapsack gives an optimistic upper bound to the 0/1 knapsack problem. There are 2 potential solutions to this if we take it as 0/1 knapsack problem,
Taking Item 1, and Item 4 gives w (Weight) = 9 and v (Value) = 13
Whereas taking Item 1, Item 2, and Item 3 also gives w = 9 and v = 13
The Fraction Solution
w = 9
v = 13.32
Which is guaranteed to be a >= to the 0/1 solution.
Optimistic Upper Bound¶
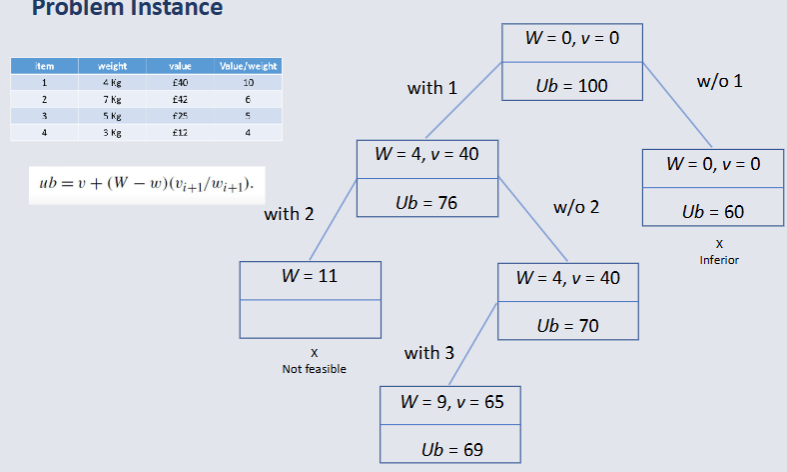
The optimistic upper bound can be used to perform Intelligent Enumeration e.g. Branch and Bound.
Branch & Bound Intelligent Enumeration¶
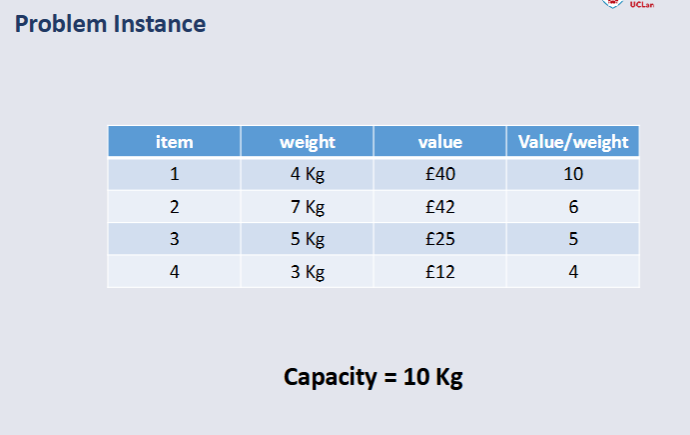

Equation Explained¶
V = Current Total of Items included so far
W = Maximum Weight Capacity of the knapsack
w = Current total weight of the items included
vi + 1 = Value of the next item that could be considered for inclusion
wi + 1 = Weight of the next item.

![[Problem Instance W-O 1#.png]]
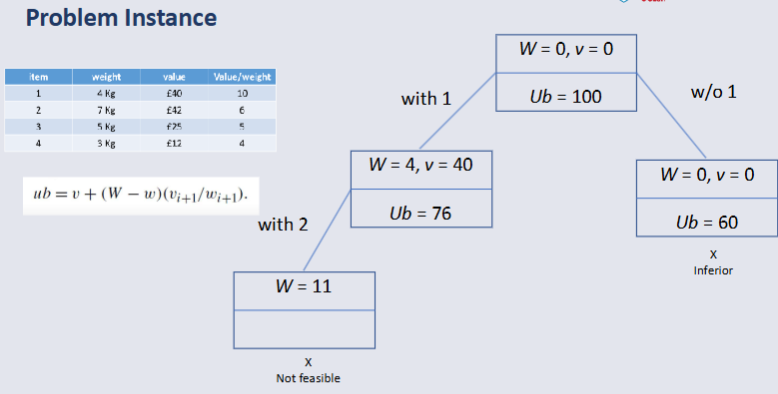
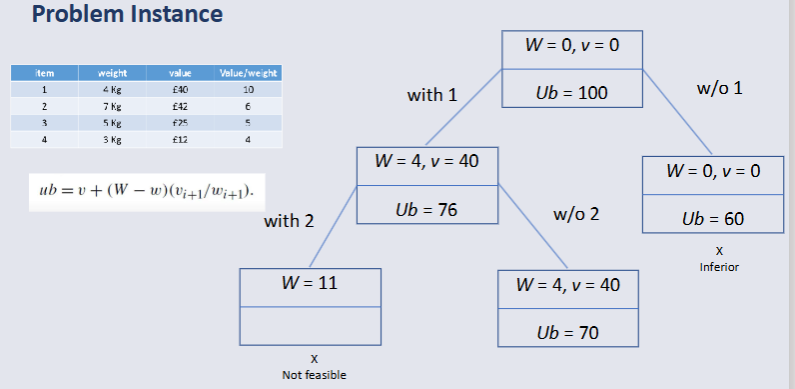

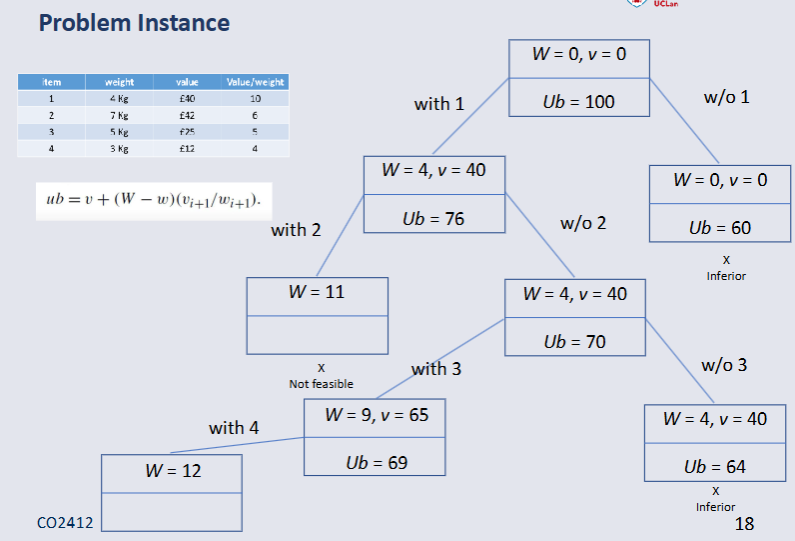
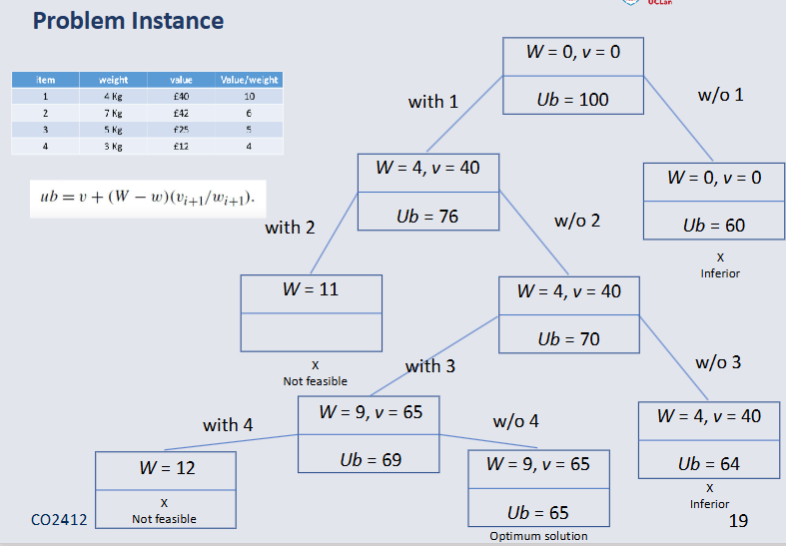
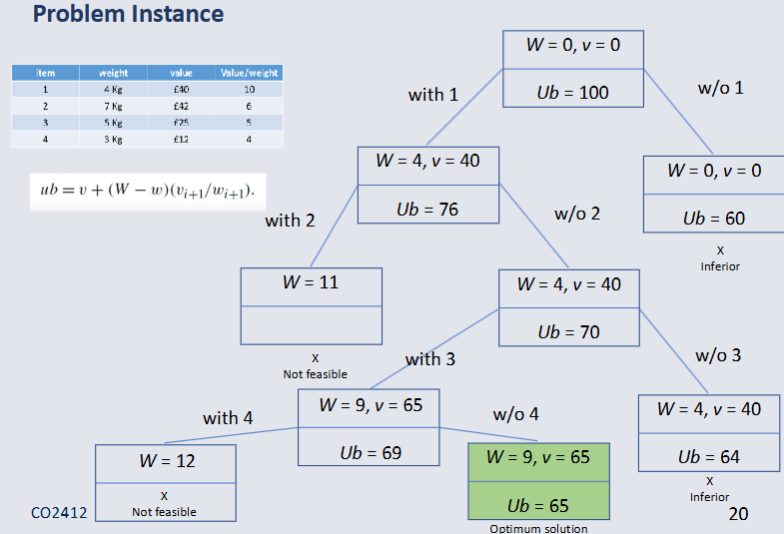
Conclusion¶
Branch and Bound is intelligent Enumeration.
We can prune any nodes where optimistic bound is less than the current best value.
Worse case is still O(2^n).
Average and best case may be significantly better.