CO2412 Computational Thinking Contents
Lecture 5 - Greedy Branch Bound

Lecture 6 - Recursive Backtacking.pdf

Recursive Backtracking¶

Backtracking involves building a solution incrementally (one piece at a time) which discards solutions that fail to satify the problems constraints.

In the worst case still O(n2) but best and average cases may be significantly better.

Simple Backtracking Walkthrough¶

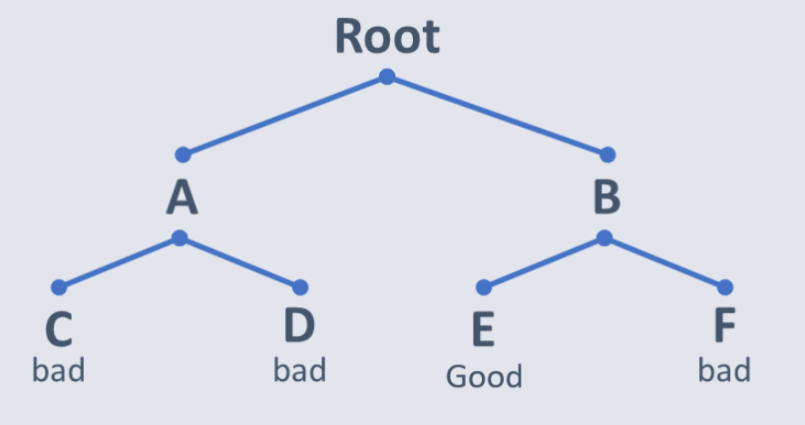
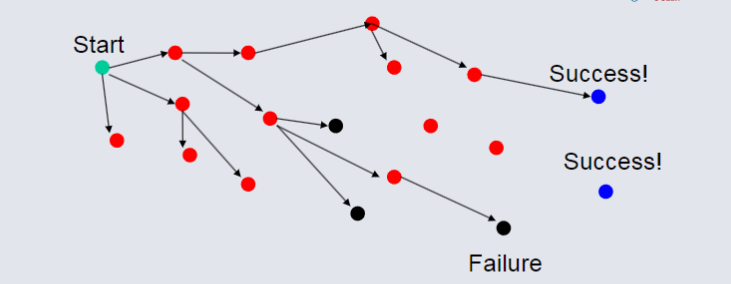
If a node only leads to failure go back to its "parent" node and try other alternatives. In the event all of these result in failure then even further backtracking may be necessary to find the most optimal with best success result.

Sudoku Example¶

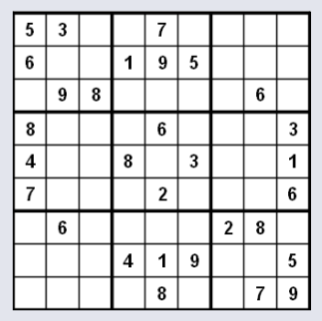
Sudoku Rules¶

Sudoku is a logic-based number placement puzzle with the following rules:
- Played on a 9x9 matrix, divided into mini matrices (3x3 sub-grids).
- Each row, column, and sub-grid must contain the numbers 1–9 exactly once.
- Duplicate numbers and values outside the range 1–9 are not allowed.
The Goal of Sudoku is that each row, each column, and each mini matrix must contain the numbers between 1 and 9 once each.

Duplicates are not allowed and only the values between 1 and 9 can be placed within each mini matrix.

Brute-Force Sudoku Solution¶

A brute algorithm is simple but a general approach.

Brute-Force Method¶

Try all combinations until finding one that works. While not a clever approach computer's are fast.

Steps in the Brute-Force Method:¶

1. If all cells are filled, the solution is complete.
2. Scan the matrix left-to-right, top-to-bottom, for the first empty cell.
3. Cycle through digits 1–9 and place one in the cell.
4. Check the placement against Sudoku rules:
   • Does the row, column, and sub-grid remain valid.
5. If valid, continue to the next cell; if invalid, try the next number.

Brute-Force Attempt:¶

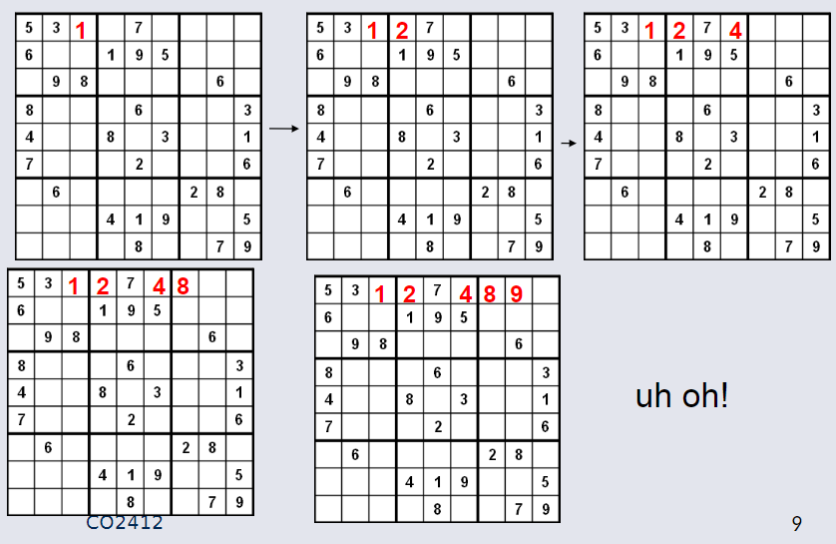
Sudoku - Dead End¶

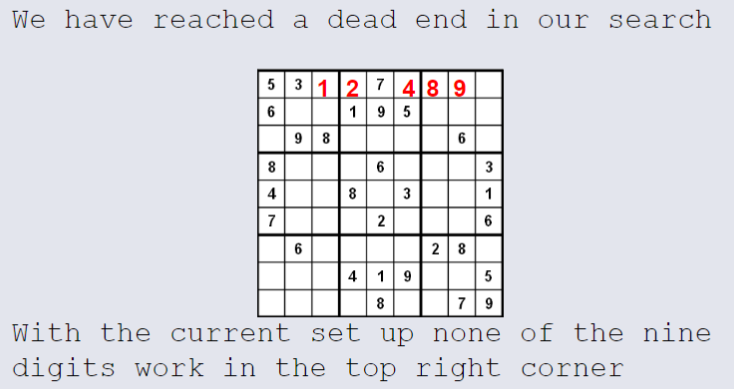
Sudoku - Backtracking¶

When the search results in a dead end, it backs up to the previous cell it was trying to fill and goes onto the next digit.

Backing up to the cell with a 9 and that turns out to be a dead end, as well so backup again.

Now the cell with the 8, trying again and 9 and move forward again.

Note: The algorithm needs to be aware of what digit to attempt next.

Sudoku - Recursive Backtracking¶

Problems such as Sudoku can be solved by using recursive backtracking.

The reason behind recursion being utilised here is due to the fact, that later versions of the problem are the same as the original problem and the reason for backtracking entirely is to test and approach different alternative solutions.

Simple Backtracking - Python Example¶

bool solve(n): # n = Node
    if n == "leaf": # Leaf being a Goal Node.
        return True
    else:
        return False

An Example of the N-Queens Problem¶

Place n queens on a chessboard so that No Queen can attack another.

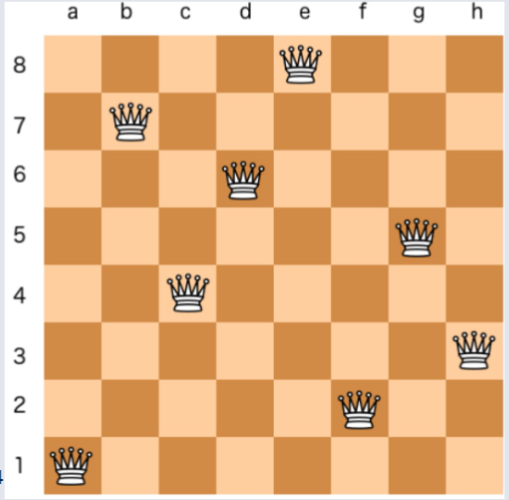
Solving N Queens Problem with Backtracking (4x4 Grid)¶

Step-By-Step Backtracking Algorithm¶

1) Start in the leftmost column
2) If all queens are placed then return true

The third step involves trying all the rows in the current column for the following:

a) If the queen can be placed safely in this row then mark this [row, column] as part of the solution and recursively check if placing queen here leads to a solution.

b) If placing the queen in [row, column] leads to a solution then return true.

c) If placing queen doesn't lead to a solution then unmark this [row, column] (Backtrack) and go to step (a) to try other rows.

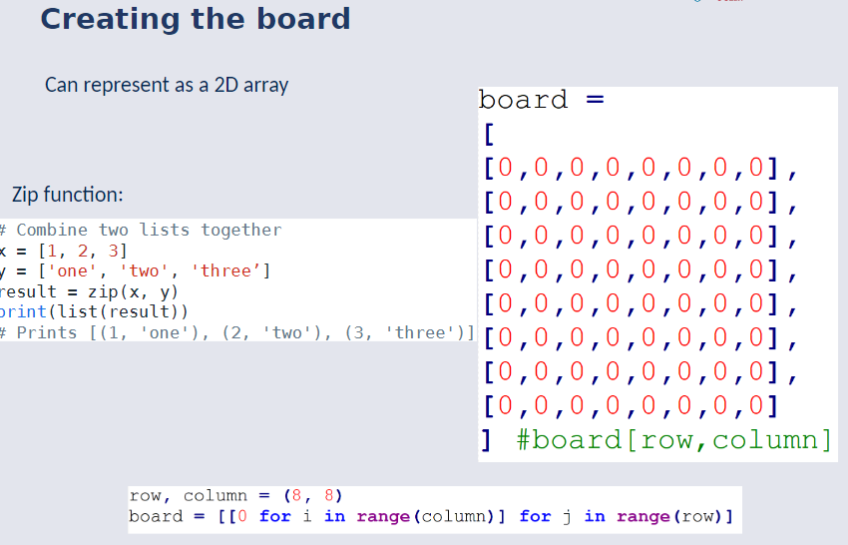
Creating The Board¶

Can be represented as a 2D array.

Another Backtracking Problem¶

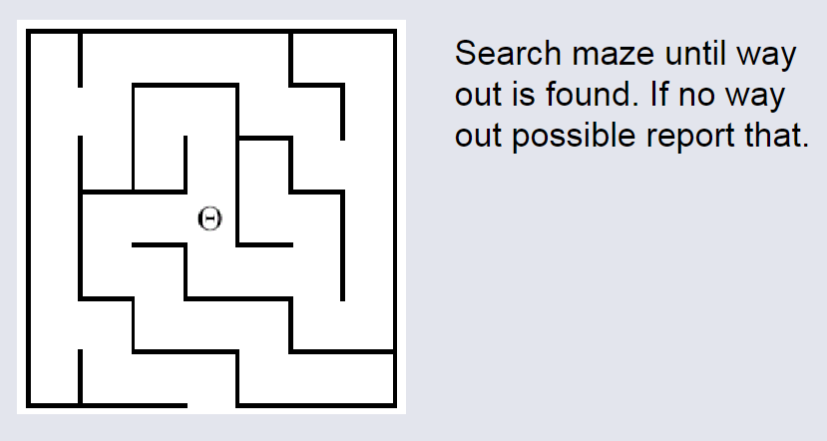
Other Challenges¶

• It may not always be straightforward to identify all the child states. For example, generating the end game in a chess solver can be difficult due to the amount of permutations.
• Requests some sort of suitable data structure and an appropriate search strategy.

Lecture 7 - Binary Search Trees & Heaps