CO2412 Computational Thinking Contents
Lecture 6 - Recursive Backtracking

Lecture 7 - Binary Search Trees and Heaps.pdf

Binary Search Trees & Heaps¶

Arrays¶

Arrays are common data structures in many programming languages.

Arrays have the following benefits:
- Easy to implement
- Easy to transverse
- Memory efficient
- Common look up times when an element is accessed/deleted/amended by index

Inserting into an array¶

Inserting an element anywhere other than the end of the list is an expensive process.

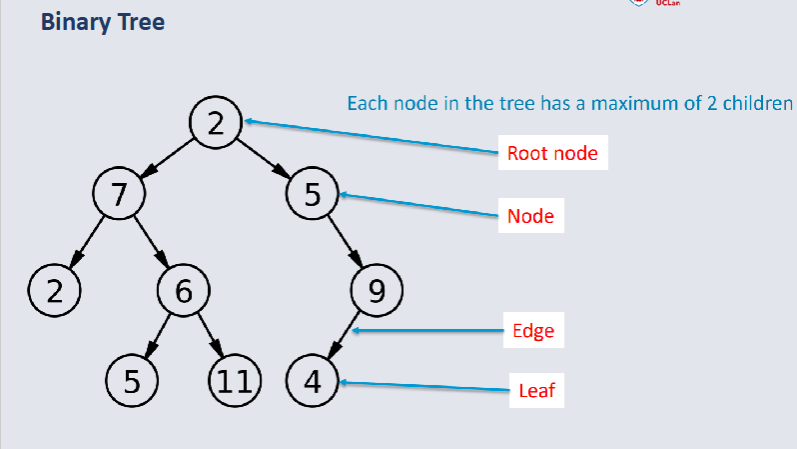
Binary Tree¶

Binary Tree

In computer science, a binary tree is a tree data structure, where each node has two children referred to as the left child and right child.

Binary Search Trees (BST) - A Sorted Binary Tree¶

Data:	3	6	8	9	11	14	16
In order to benefit from the efficiency of a logarithmic time algorithm, which also supports insertion and deletion, which may be required with a different data structure; the Binary Search Tree (BST).
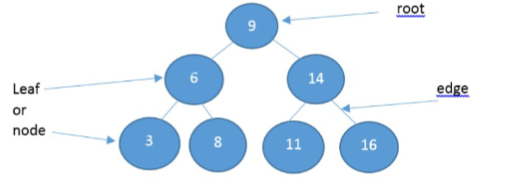To begin, the middle element in the data (9) and make it the root of the tree, which then follows the rule that:
- values lower than the root (9) will be placed in nodes to the left of the tree and values greater than the root are placed to the right.

This process is continued for all sub-trees created.

Searching Binary Search Tree¶

To find the value 8 as an example.

Step-By-Step Search¶

1) start at the root (9) of the tree.
2) Is the value trying to be found (8) less than or greater than the root.
3) Since it can be concluded that 8 is less than 9
4) Then since that value is lower, look at the root and check the node to its left (the lower value)
5) Check whether that is smaller or larger than the value 8. Which it is
6) Following the tree leads us to the conclusive answer of 8

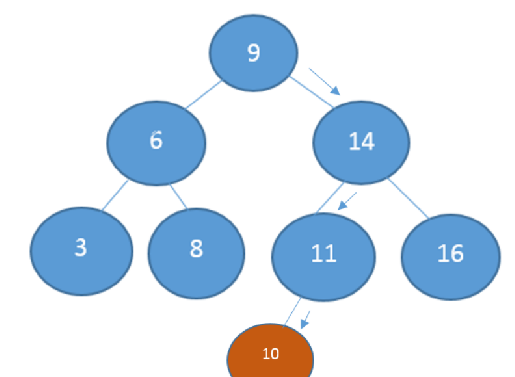
The same process can be taken to deduce that a number does not exist in the tree. For example, if the number 10 is trying to be found, a number that doesn't exist in the tree.

As shown when following the process detailed in the steps:
1) Start at the root 9
2) 10 is bigger than 9 so check to the right
3) 10 is less than 14 so check to the left
4) However since there is nothing below 11 it can be concluded that 10 doesn't exist in the tree

To insert 10 into the binary tree, the same process is continued:
5) 10 is smaller than 11 so check the left
6) Insert the element in its correct place to the left of the node containing 11

Deletion is a slightly more complicated process and has a few more operations but is essentially the same.

Full Binary Tree¶

A full binary tree is a type of binary tree in which:
- Every node either has 0 or 2 children.
- No node has only one child.

In a full binary tree, if the total number of nodes is (n), the height (h) of the tree (or the longest path from the root to a leaf) is proportional to (log(n)).

This relationship arises because the number of nodes at each level doubles as you move down the tree.

Considerations¶

Care needs to be taken when structuring the tree. Simply sorting nodes in a sorted order may result in the tree becoming unbalanced.

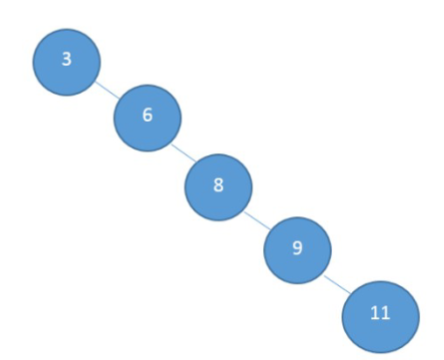
At which point the time taken, to insert or delete an item becomes linear O(n).

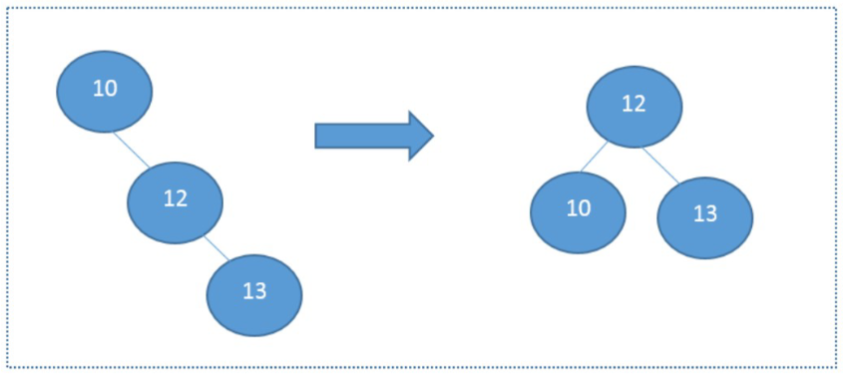
Reconstructing the Tree¶

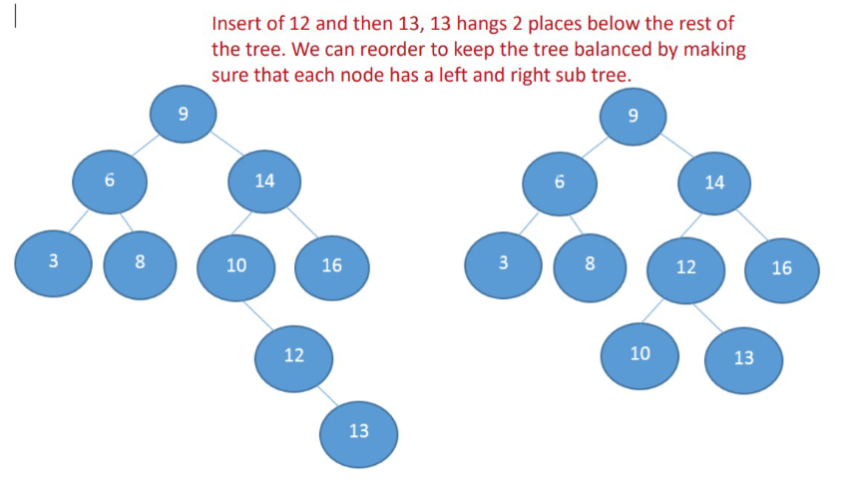
Rebalancing Example¶

Tree Arithmetic¶

To calculate the number of nodes in the tree:
Formula: 2 ^ height - 1

To calculate the number of nodes on a level off the tree:
Formula: 2^(Level On Tree - 1))

Tree Class¶

# Class to implement basic tree data structure

class Tree_Node:
    def __init__(self, data, children=[]):
        self.data = data
        self.children = children

    def __str__(self, level=0):
        ret = " " * level + str(self.data) + "\n"
        for child in self.children:
            ret += child.__str__(level + 1)
        return ret

    def add_child(self, TreeNode):
        self.children.append(TreeNode)

# Example Usage
# Categories:
tree = TreeNode('Drinks')
cold = TreeNode('Cold')
hot = TreeNode('Hot')
tree.add_child(cold)
tree.add_child(hot)

# Types of Drinks
tea = TreeNode("Tea")
coffee = TreeNode("Coffee")
coke = TreeNode("Coke")
hot.add_child(tea)
hot.add_child(coffee)
cold.add_child(coke)

print(tree)

Output¶

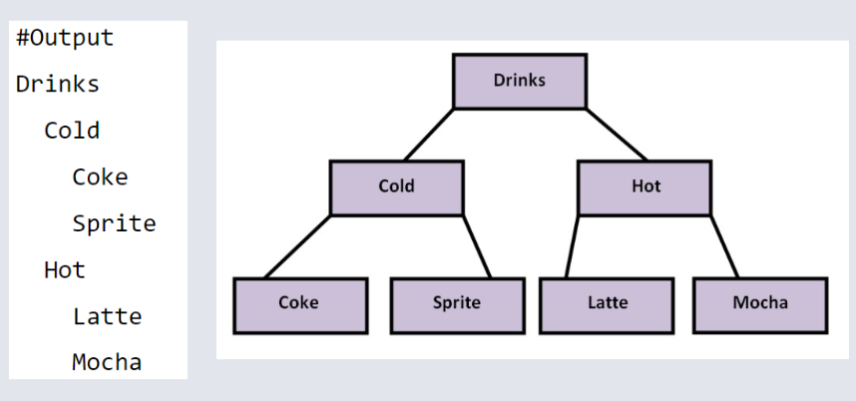
The diagram on the right side is just a physical indicator of the tree structure created.

Summary¶

Binary search trees are an alternative data structure to an array.

Worst Case Efficiency is log n for search, insertion, deletion if the tree is balanced or near balanced.

Requires some maintenance and care in the way the elements are inserted or the tree may become unbalanced.

An unbalanced tree tends towards a linear rather than logarithmic worse case: O(n)

Lecture 8 - Graph Theory