CO2412 Computational Thinking Contents
Lecture 7 - Binary Search Trees & Heaps
Graph Theory¶
What is a Graph?¶
A visual representation of a set of objects where some of these objects are connected.
The objects are represented by points called vertices and the links that connect the objects are known as edges.
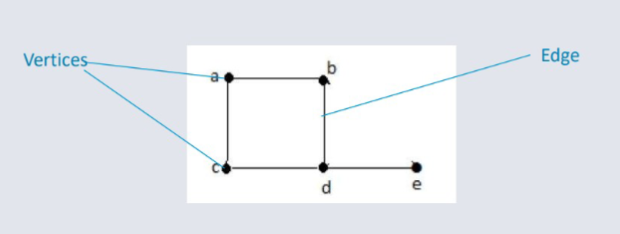
A Formal Definition¶
A graph G can be defined as
- G = (V, E)
V is the set of vertices in the group.
E is the set of edges connecting the vertices.
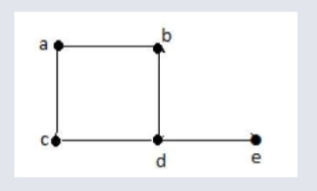
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
NB for a non-directional graph.
ab & ba are the same. Sets do not include repetition and the edge is only included once.
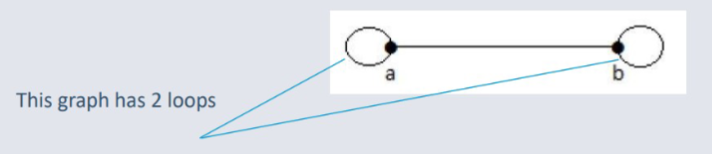
Loops¶
A loop occurs when an edge connects a vertex back to itself.
For example, an edge drawn from (a) to (b) would be considered a loop.
Degree of Vertex (Valency)¶
The degree of a vertex (dot) is the number of edges (lines) connected to it.
This is denoted by (deg(V)), where (V) is the vertex in question.
For example, if a vertex has two edges, its degree would be 2.
The Degree Of Vertex for the Vertex (A) is:
deg(a) = 2 (2 edges connected to it)
deg(b) = 2
deg(c) = 2
deg(d) = 3
deg(e) = 1
A Vertex with only 1 degree of vertex is known as the Pendent Vertex.
A loop in a graph counts as having a Valency (Degree of Vertex Number) of 2.
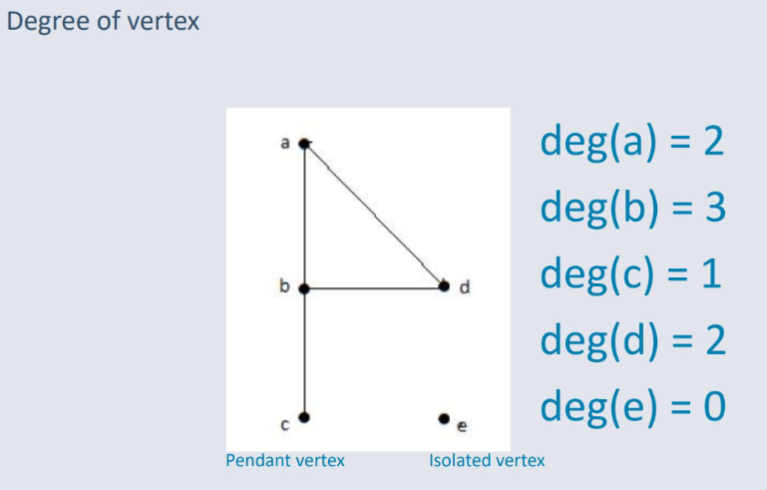
In this case deg(e) = 0 and therefore, a vertex with 0 Valency is known as an Isolated Vertex.
Degree Sequence¶
Valency can also be displayed as a degree sequence.
For graph G with the following Degree of Vertex (Valency):
- deg(a) = 2
- deg(b) = 3
- deg(c) = 1 (Pendent Vertex)
- deg(d) = 2
- deg(e) = 0 (Isolated Vertex)
The Degree Sequence is as follows:
Degree Sequence = {2, 3, 1, 2, 0} (The amount of edges for every vertex in the graph.
Directed Graphs¶
For a directed graph, the edges connecting the vertices have a direction associated with them.
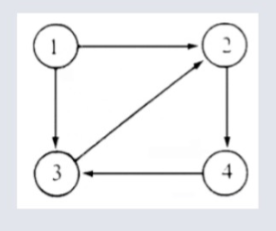
Degree of Vertex for Directed Graphs¶
In a directed graph each vertex has an indegree and outdegree, their purpose is as follows:
- Indegree is the number of edges coming into the vertex. Denoted by deg+(V)
- Outdegree is the number of edges leaving the vertex. Denoted by deg-(V)
Directed Graph Valency¶
Indegrees:
deg(1) = 0 (Isolated Vertex)
deg(2) = 2
deg(3) = 2
deg(4) = 1 (Pendent Vertex)
Outdegrees:
deg(1) = 2
deg(2) = 1 (Pendent Vertex)
deg(3) = 1 (Pendent Vertex)
deg(4) = 1 (Pendent Vertex)
Degree of Sequence:¶
Degree of Sequence = {0, 2, 2, 1, 2, 1, 1, 1} (Indegrees, Outdegrees)
Weighted Graph¶
A Weighted Graph is a graph in which each branch is given a numerical weight.
A weighted graph is therefore a special type of labelled graph in which the labels are numbers.
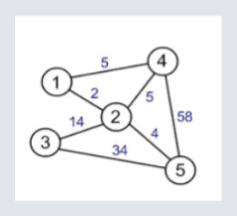
Simple Graphs¶
A Simple Graph is an unweighted, undirected graph containing no graph loops, or multiple edges. Therefore, a simple graph may be either connected or disconnected.
Applications of Graph Theory¶
Examples usages of Graph Theory:
Electrical Engineering
Used For: Designing Circuit Connections.
Computer Science
Used For: Study of algorithms such as:
- Kruskal's Algorithm
- Pim's Algorithm
- Dijkstra's Algorithm
Computer Networks
Used For: Relationships between interconnected computers in the network.
Science
Used For: Molecular and Chemical Structure of a substance i.e. DNS structure of an organism.
Google Maps Graph Example¶
Google Maps is one large graph with the aforementioned Vertices and Edges.
Google utilises an algorithm, such as Dijkstra's Algorithm to calculate the shortest path between 2 vertices.
In this example:
- Vertices represent locations, such as intersections, landmarks, or specific addresses
- Edges represent the connections or roads between the locations.
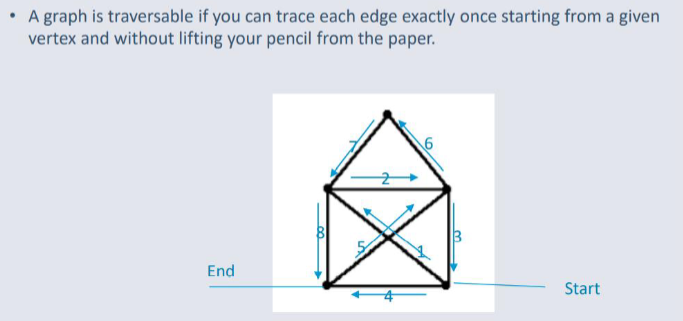
Traversable Graphs¶
A graph is Traversable if a path can be traced between all vertices without retracing the same path.
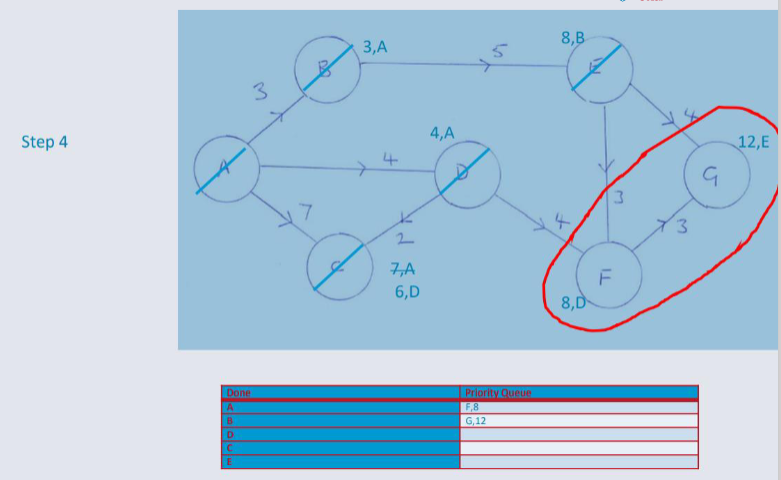
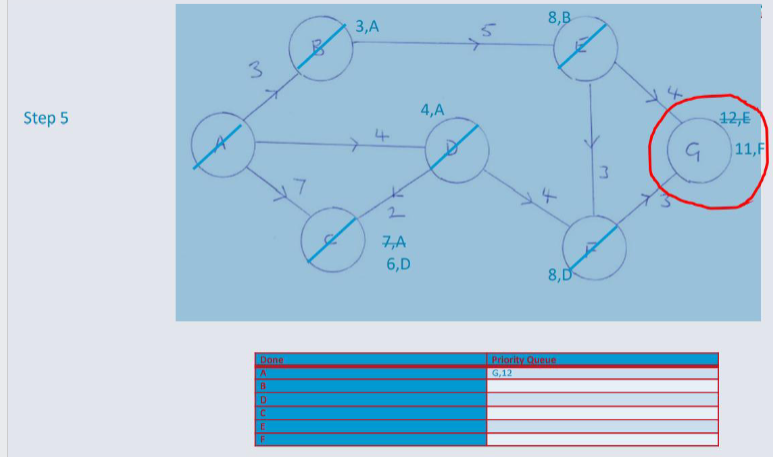
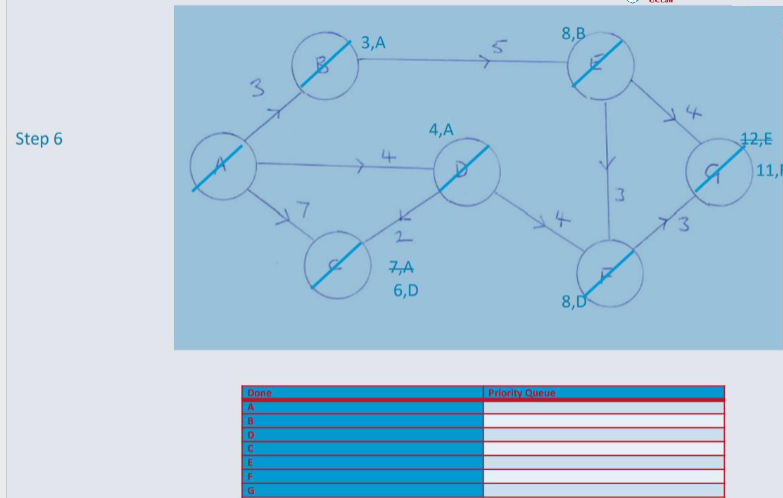
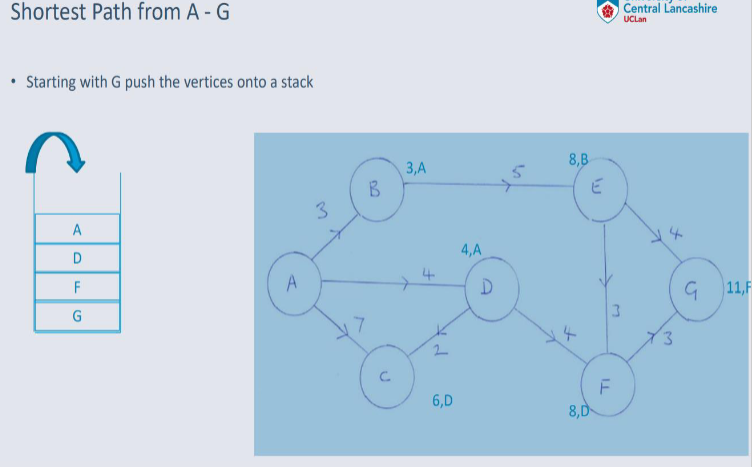
Dijkstra's Algorithm¶
An algorithm designed for finding the shortest path between nodes in a weighted, possibly directed graph.
e.g. A Road Network
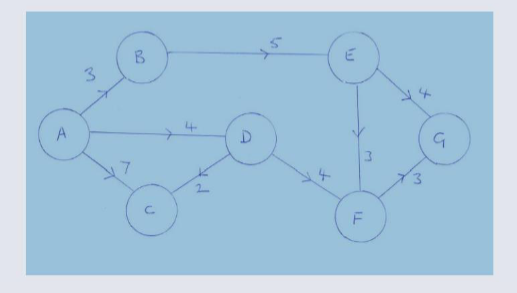
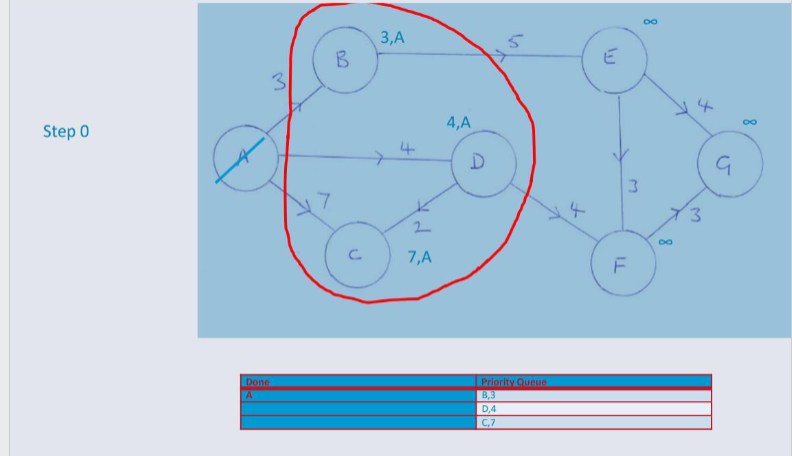
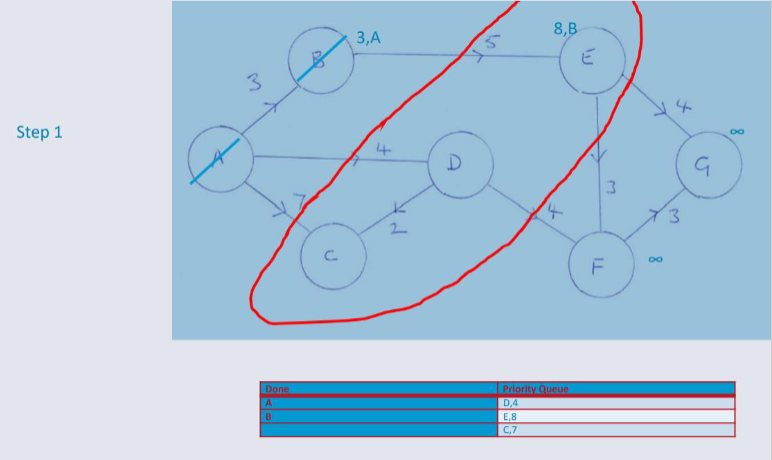
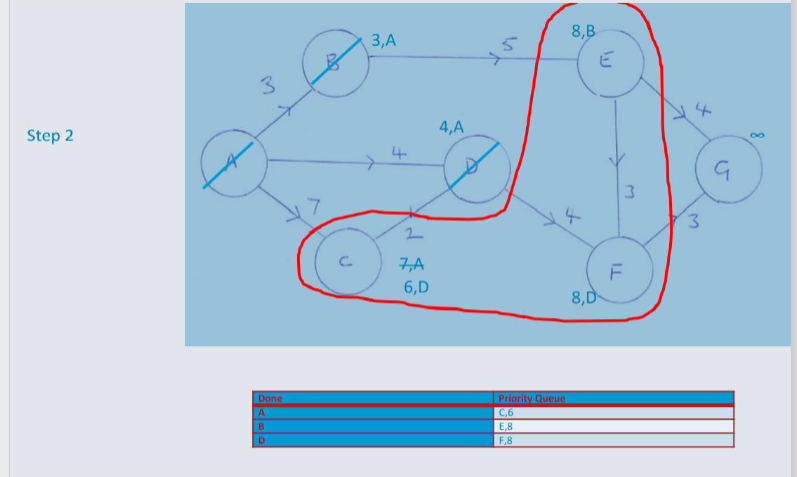
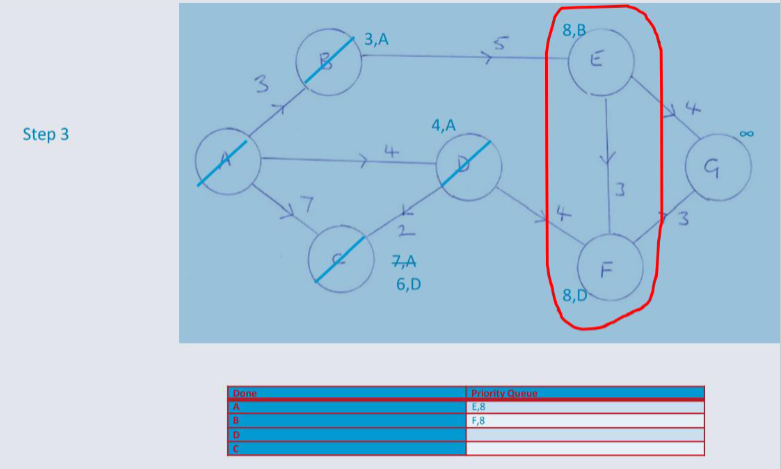
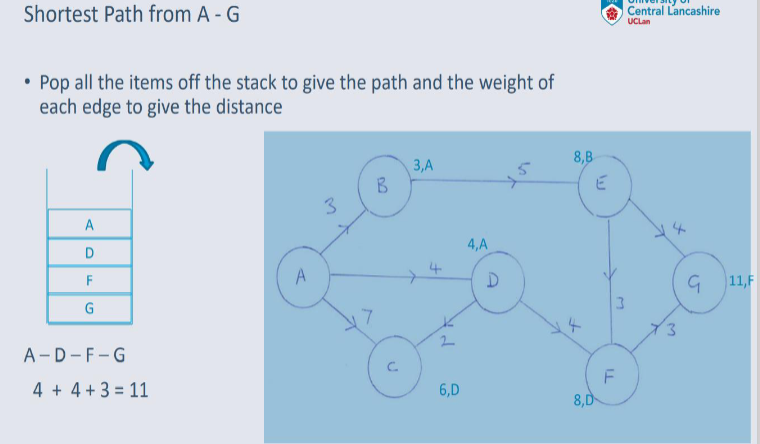
Greedy Algorithm¶
Dijkstra's algorithm, adopts a Greedy Approach to solving the shortest path problem.
At each stage of the process, the best option available is taken. (The edge will the lowest weight).
Unlike the 0/1 Knapsack problem where the Greedy algorithm is not guaranteed to return an optimal solution. However, in this circumstance Greedy returns an optimal solution to the shortest path problem.